La esperanza matemática o valor esperado de una variable aleatoria discreta es la suma del producto de la probabilidad de cada suceso por el valor de dicho suceso.
Hacen referencia a la ganancia promedio esperada por un jugador cuando hace un gran número de apuestas.
Si E(x) = 0 no existe ventaja ni para el jugador ni para la banca.
EJEMPLOS:
- Si una persona compra una papeleta en una rifa, en la que puede ganar de 5.000 € ó un segundo premio de 2000 € con probabilidades de: 0.001 y 0.003. ¿Cuál sería el precio justo a pagar por la papeleta?
E(x) = 5000 · 0.001 + 2000 · 0.003 = 11
Un jugador lanza dos monedas. Gana 1 ó 2 € si aparecen una o dos caras. Por otra parte pierde 5 € si no aparece cara. Determinar la esperanza matemática del juego y si éste es favorable.
E = {(c,c);(c,x);(x,c);(x,x)}
p(+1) = 2/4
p(+2) = 1/4
p(−5) = 1/4
E(x)= 1 · 2/4 + 2 · 1/4 - 5 · 1/4 = -1/4 (DESFAVORABLE)
DISTRIBUCIÓN DE PROBABILIDAD DE VARIABLES ALEATORIAS DISCRETAS:
Una variable aleatoria es discreta cuando sólo puede tomar unos ciertos valores enteros.
Ejemplos de variable aleatoria
• Número de caras obtenidas al lanzar tres monedas: 0, 1, 2, 3.
• Suma de las caras superiores obtenidas al lanzar dos dados: 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12.
FORMAS DE REPRESENTAR GRAFICAMENTE:
- La distribución de Bernoulli, que toma valores "1", con probabilidad p, o "0", con probabilidad q = 1 − p.
- La distribución de Rademacher, que toma valores "1" o "-1" con probabilidad 1/2 cada uno.
- La distribución binomial, que describe el número de aciertos en una serie de n experimentos independientes con posibles resultados "sí" o "no" (ensayo de Bernoulli, todos ellos con probabilidad de acierto p y probabilidad de fallo q = 1 − p.
- La distribución binomial de Poisson, que describe el número de aciertos en una serie de n experimentos independientes con posibles resultados "sí" o "no", cada uno de ellos con probabilidad de éxito distinta y definida por una secuencia finita p1, p2... pn.
- La distribución beta-binomial, que describe el número de aciertos en una serie de n experimentos independientes con posibles resultados "sí" o "no", cada uno de ellos con una probabilidad de acierto variable definida por una beta.
- La distribución degenerada en x0, en la que X toma el valor x0 con probabilidad 1. A pesar de que no parece una variable aleatoria, la distribución satisface todos los requisitos para ser considerada como tal.
- La distribución uniforme discreta, en el que todos los resultados posibles forman de un conjunto finito en el que todos son igualmente probables. Esta distribución describe el comportamiento aleatorio de una moneda, un dado o una ruleta de casino equilibrados (sin sesgo).
- La distribución hipergeométrica, que mide la probabilidad de obtener x (0 ≤ x ≤ d) elementos de una determinada clase formada por d elementos pertenecientes a una población de N elementos, tomando una muestra de n elementos de la población sin reemplazo.
- distribución hipergeométrica no central de Fisher.
- distribución hipergeométrica no central de Wallenius.
- La ley de Benford, que describe la frecuencia del primer dígito de un conjunto de números en notación decimal.
EJEMPLO RESUELTO:
Lanzamos un dado perfecto 240 veces, anotamos el resultado obtenido en la cara superior obteniendo los siguientes resultados:
| Distribución aleatoria discreta | ||||||
|---|---|---|---|---|---|---|
| Cara superior | 1 | 2 | 3 | 4 | 5 | 6 |
| Número de veces | 40 | 39 | 42 | 38 | 42 | 39 |
1. Tabla de distribución de frecuencias
La tabla de distribución de frecuencias muestra los resultados obtenidos
2. Tabla de distribución de probabilidad
La tabla de distribución de probabilidad muestra los resultados esperados
3. Gráfica de las distribuciones
En la gráfica de los valores esperados, observamos que a cada valor de la variables aleatoria xi "cara del dado" le hacemos corresponder su probabilidad teórica. A esta ley se le llama distribución de probabilidad.
DISTRIBUCIÓN BINOMIAL:
La distribución binomial es una distribución de probabilidad discreta que cuenta el número de exitos en una secuencia de n ensayos de Bernoulli independientes entre sí, con una probabilidad fija p de ocurrencia del éxito entre los ensayos. Un experimento de Bernoulli se caracteriza por ser dicotómico, esto es, sólo son posibles dos resultados. A uno de estos se denomina éxito y tiene una probabilidad de ocurrencia p y al otro, fracaso, con una probabilidad q = 1 - p. En la distribución binomial el anterior experimento se repite n veces, de forma independiente, y se trata de calcular la probabilidad de un determinado número de éxitos. Para n = 1, la binomial se convierte, de hecho, en una distribución de Bernoulli.
Para representar que una variable aleatoria X sigue una distribución binomial de parámetros n y p, se escribe:
Ejemplos:
- Se lanza un dado diez veces y se cuenta el número X de tres obtenidos: entonces X ~ B(10, 1/6)
- Se lanza una moneda dos veces y se cuenta el número X de caras obtenidas: entonces X ~ B(2, 1/2)
Supongamos que se lanza un dado (con 6 caras) 50 veces y queremos conocer la probabilidad de que el número 3 salga 20 veces. En este caso tenemos una X ~ B(50, 1/6) y la probabilidad sería P(X=20):
Las siguientes situaciones son ejemplos de experimentos que pueden modelizarse por esta distribución:
DISTRIBUCIÓN HIPERGEOMÉTRICA:
En teoría de la probabilidad la distribución hipergeométrica es una distribución discreta relacionada con muestreos aleatorios y sin reemplazo. Supóngase que se tiene una población de N elementos de los cuales, d pertenecen a la categoría A y N-d a la B. La distribución hipergeométrica mide la probabilidad de obtener x (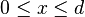
) elementos de la categoría A en una muestra sin reemplazo de n elementos de la población original.
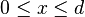) elementos de la categoría A en una muestra sin reemplazo de n elementos de la población original.
La función de probabilidad de una variable aleatoria con distribución hipergeométrica puede deducirse a través de razonamientos combinatorios y es igual a
donde 
es el tamaño de población, 
es el tamaño de la muestra extraída, 
es el número de elementos en la población original que pertenecen a la categoría deseada y 
es el número de elementos en la muestra que pertenecen a dicha categoría. La notación 
hace referencia al coeficiente binomial, es decir, el número de combinaciones posibles al seleccionar elementos de un total 
.
es el tamaño de población, es el tamaño de la muestra extraída, es el número de elementos en la población original que pertenecen a la categoría deseada y es el número de elementos en la muestra que pertenecen a dicha categoría. La notación hace referencia al coeficiente binomial, es decir, el número de combinaciones posibles al seleccionar elementos de un total .
El valor esperado de una variable aleatoria X que sigue la distribución hipergeométrica es
![E[X]=\frac{nd}{N}](http://upload.wikimedia.org/math/e/d/b/edb7931c237719680795389c71e2ca37.png)
y su varianza,
![Var[X]=\bigg(\frac{N-n}{N-1}\bigg)\bigg(\frac{nd}{N}\bigg)\bigg( 1-\frac{d}{N}\bigg).](http://upload.wikimedia.org/math/9/b/2/9b21150dd51ee2e8e3c219b9d6c67cdd.png)
En la fórmula anterior, definiendo
se obtiene
![Var[X]=npq\frac{N-n}{N-1}.](http://upload.wikimedia.org/math/8/4/5/8450776365971ac3ed36f95d91b68b22.png)
La distribución hipergeométrica es aplicable a muestreos sin reemplazo y la binomial a muestreos con reemplazo. En situaciones en las que el número esperado de repeticiones en el muestreo es presumiblemente bajo, puede aproximarse la primera por la segunda. Esto es así cuando N es grande y el tamaño relativo de la muestra extraída, n/N, es pequeño.
EJEMPLOS
- De un lote de 10 proyectiles, 4 se seleccionan al azar y se disparan. Si el lote contiene 3 proyectiles defectuosos que no explotarán, ¿cuál es la probabilidad de que , a) los 4 exploten?, b) al menos 2 no exploten?
Solución:
a) N = 10 proyectiles en total
a = 7 proyectiles que explotan
n = 4 proyectiles seleccionados
x = 0, 1, 2, 3 o 4 proyectiles que explotan = variable que nos define el número de proyectiles que explotan entre la muestra que se dispara
b) N = 10 proyectiles en total
a = 3 proyectiles que no explotan
n = 4 proyectiles seleccionados
x = 0, 1, 2 o 3 proyectiles que no explotan
p(al menos 2 no exploten) = p( 2 o más proyectiles no exploten) = p(x = 2 o 3; n=4) =
- a)¿Cuál es la probabilidad de que una mesera se rehúse a servir bebidas alcohólicas únicamente a dos menores de edad si verifica aleatoriamente solo 5 identificaciones de entre 9 estudiantes, de los cuales 4 no tienen la edad suficiente?, b) ¿Cúal es la probabilidad de que como máximo 2 de las identificaciones pertenezcan a menores de edad?
Solución:
a) N = 9 total de estudiantes
a = 4 estudiantes menores de edad
n = 5 identificaciones seleccionadas
x = variable que nos define el número de identificaciones que pertenecen a personas menores de edad
b) N = 9 total de estudiantes
a = 4 estudiantes menores de edad
n = 5 identificaciones seleccionadas
x = variable que nos define el número de identificaciones que pertenecen a personas menores de edad
x = 0, 1, 2, 3 o 4 identificaciones de personas menores de edad
